본 포스팅은 밑바닥부터 시작하는 딥러닝3 책의 내용을 공부한 후 개인적으로 중요하다고 생각되는 내용들을 정리하는 것이 목적입니다.
해당 책은 큰 맥락을 '고지'로 나누고 있으며 총 5고지가 있으며 각 고지의 세부 내용을 'step'으로 분리해서 학습합니다.
1개의 고지를 학습하고 포스팅 할 경우 내용이 너무 길어져 가독성 측면을 고려해 각 고지의 절반에 해당하는 내용들을 하나의 포스팅에서 다룰 예정입니다. 혹시 틀린 내용이 있다면 피드백은 항상 환영입니다🤗

Step1. 상자로서의 변수
프로그래밍에서 흔히 변수는 상자라는 개념을 통해 설명되곤 한다.
변수를 상자안에 넣는다는 개념에서 살펴보면 다음과 같이 변수의 성질을 제법 잘 보여준다.
- 상자와 데이터는 별개다.
- 상자에는 데이터가 들어간다. (대입 또는 할당한다)
- 상자 속을 들여다보면 데이터를 알 수 있다. (참조한다)

변수라는 개념은 앞으로 다룰 내용에서 가장 중요한 개념이니 확실히 알아두도록 하자.
상자라는 변수에 값을 대입한다는 위의 내용을 코드로 구현하면 다음과 같다.
class Variable():
def __init__(self, data):
self.data = data
머신러닝 시스템은 기본 데이터 구조로 '다차원 배열'을 사용한다. 그래서 Variable 클래스는 넘파이의 다차원 배열만 취급한다.
넘파이의 다차원 배열을 통해 변수를 생성하면 다음과 같다.
import numpy as np
data = np.array(1.0)
x = Variable(data)
print(x.data)
# 실행결과
1.0
📍 다차원 배열을 다룰 때 주의해야 할 점이 있는데 '벡터'의 차원이 몇이냐라고 한다면 a = [1, 2, 3]과 같은 예시에서는 벡터 a의 차원은 원소의 개수인 3이 된다. 하지만 배열의 차원이 몇이냐라고 한다면 a는 1차원 벡터이므로 배열 a의 차원은 1이 된다.
Step2. 변수를 낳는 함수
위의 내용을 통해 우리는 Variable 클래스를 상자로 사용할 수 있게 되었다.
하지만 우리에겐 단순한 Variable 상자를 마법의 상자로 바꾸는 장치가 필요한데 이 때 필요한 것이 함수이다.
함수의 정의를 간단하게 살펴보면 어떠한 입력 $x$가 들어왔을 때 특정한 연산을 해주는 장치 $f$를 통해 출력값 $y$가 나오는 것으로 볼 수 있다. 이와 같이 변수 사이의 대응 관계를 정하는 역할을 함수가 맡게 되며 아래의 그림은 그 의미를 시각적으로 표현한 것이다.

위의 그림처럼 표현되는 그래프를 컴퓨터공학에서는 계산그래프(computational graph)라고 표현하며 노드(동그라미, 함수는 네모로 표시)와 엣지(화살표)로 표현된다.
함수를 코드로 표현하면 다음과 같다.
class Function():
def __call__(self, input):
x = input.data
y = self.forward(x)
output = Variable(y)
return output
def forward(self):
raise NotImplementedError()
class Square(Function):
def forward(self, x):
return x ** 2
__call__ method는 파이썬 매직메서드(magic method)에 해당하며 클래스의 인스턴스를 생성하고 해당 인스턴스를 함수처럼 호출할 때 실행되는 메서드이다. 또한 Function Class에서는 함수의 고유한 기능만을 정의하며 추후에 나올 여러 가지 함수 Square, Exp, Sin... 등을 수행하기 위해서 각 함수의 고유한 기능은 Function Class를 상속받아 forward method만 구현하도록 작성하였다.
또한 Function Class의 Input, output은 모두 Variable 인스턴스이며 이를 통해 뒤에서 나올 합성함수의 구현이 가능하도록 하였다.
Step3. 함수 연결
위의 방식으로 Function Class를 구현해둔 덕분에 다음과 같은 코드로 합성함수를 구현할 수 있게 된다.
class Exp(Function):
def forward(self, x):
return np.exp(x)
A = Square()
B = Exp()
C = Square()
x = Variable(np.array(0.5))
a = A(x)
b = B(a)
y = C(b)
print(y.data)
# 실행결과
1.648721270700128
중요한 점은 중간에 등장하는 4개의 변수 x, a, b, y 모두 Variable 인스턴스이기 때문에 Function Class의 __call__ 메서드의 입출력이 Variable 인스턴스로 통일되어 있는 덕분에 이와 같이 여러 함수를 연속하여 적용할 수 있는 것이다.

위의 그림과 같이 여러 함수를 순서대로 적용하여 만들어진 변환 전체를 하나의 큰 함수로 볼 수 있다.
이처럼 여러 함수로 구성된 함수를 합성함수 라고 한다. 합성 함수를 구성하는 각 함수의 계산은 간단하더라도, 연속으로 적용하면 더 복잡한 계산도 해낼 수 있다는 것이 중요하다.
Step4. 수치 미분
미분에 대한 자세한 내용은 본 포스팅에서 다루지 않겠지만 미분값을 구하는 방법 중에는 '전진 차분'(numerical differentiation)과 '중앙 차분'이 있다.
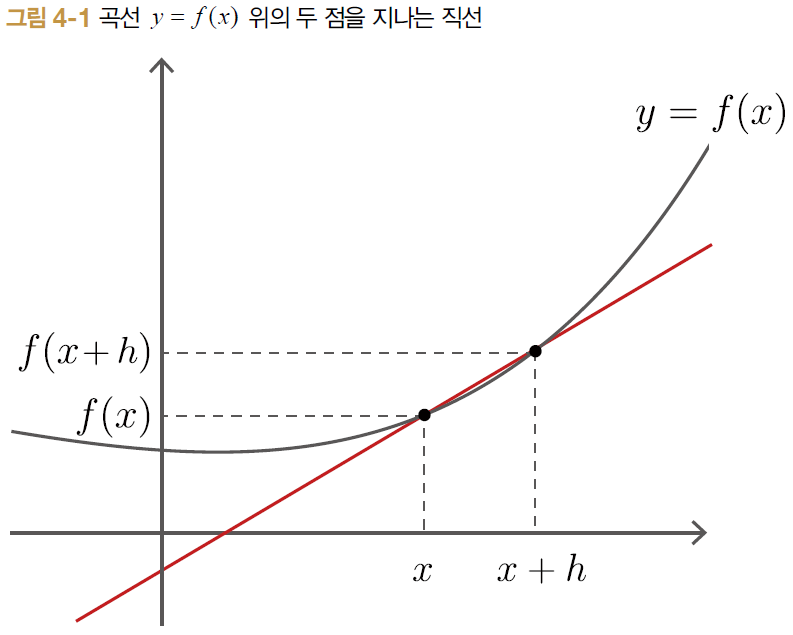

전진 차분은 위의 그림에서 볼 수 있듯이 $x$와 $x+h$ 지점에서 기울기를 구하는 방식이고, 중앙 차분은 $x-h$와 $x+h$의 지점에서 기울기를 구하는 방식이다. 중앙 차분이 전진 차분에 비해 상대적으로 오차가 작다. 증명까지는 하지 않겠지만 위의 그림에서 볼 수 있듯이 중앙 차분이 전진 차분보다 진정한 미분의 기울기와 비슷한 것을 볼 수 있다.
중앙 차분의 수식은 $\frac{f(x+h) - f(x-h)}{2h}$와 같고 이 수식을 코드로 구현하면 다음과 같다.
def numerical_diff(f, x, eps=1e-4):
x0 = Variable(x.data - eps)
x1 = Variable(x.data + eps)
y0 = f(x0)
y1 = f(x1)
return (y1.data - y0.data) / (2 * eps)
f = Square()
x = Variable(np.array(2.0))
dy = numerical_diff(f, x)
print(dy)
# 실행결과
4.00000000004
컴퓨터에서는 극한값을 표현할 때 위의 코드와 같이 0.0001과 같은 매우 작은 수로 대체해서 사용한다.
실제 해석적으로 $x^2$을 미분한다면 $2x$가 되고 미분값은 4가 되고 중앙 차분의 결괏값과 비교해 봤을 때 오차는 발생하지만 그 크기가 매우 작은 것을 알 수 있다.
위의 수치미분을 통한 방식의 장점으로는 구현이 쉽고 거의 정확한 값을 얻을 수 있지만 단점으로는 변수가 여러개인 계산을 미분할 경우 변수 각각을 미분해야 하기 때문에 계산량이 많아진다. 특히 딥러닝에서는 파라미터의 수가 몇 백만에서 몇 천만까지 있는 경우가 많은데 이 모두를 수치 미분으로 계산한다는 것은 현실적이지 않다. 따라서 등장한 것이 바로 '역전파'이며 다음 포스팅에서 계속 알아보도록 하겠다.
'AI Development > PyTorch' 카테고리의 다른 글
| 밑바닥부터 시작하는 딥러닝3 - Dezero의 도전(3) (0) | 2024.02.23 |
|---|---|
| 밑바닥부터 시작하는 딥러닝3 - Dezero의 도전(2) (1) | 2024.02.23 |
| 밑바닥부터 시작하는 딥러닝3 - Dezero의 도전(1) (0) | 2024.02.22 |
| 밑바닥부터 시작하는 딥러닝 3 - 자연스러운 코드로(1) (0) | 2024.02.03 |
| 밑바닥부터 시작하는 딥러닝 3 - 미분 자동 계산(2) (0) | 2024.02.01 |
