T-test
두 집단의 평균을 비교할 때 t-test를 사용한다.
두 집단의 평균이 다른지를 비교할때는 이표본 t-검정(two sample t-test)를 사용하고 같은지 다른지를 보는 양측 검정(p1 != p2)을 수행한다.
만약 한 집단의 평균이 특정 값인지를 검정하고 싶다면 단일 표본 t-검정(one sample t-test)를 사용한다. 대응표본 t-검정(paired t-test)는 실질적으로 단일 표본 t-검정과 동일하다.
집단 A와 집단 B의 평균을 비교한다고 할 때, two sample t-test의 원리는 집단A의 평균과 집단B의 평균의 차가 t분포를 따른다는 가정하에, 그것이 통계적으로 유의미하게 0과 다른지를 따지는 것이다. 따라서 귀무가설과 대립가설은 다음과 같다.
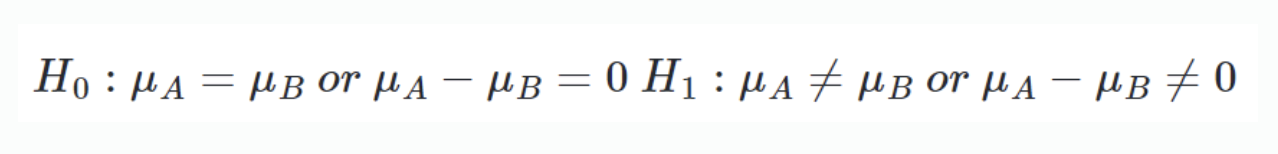
이를 검정하기 위해서, 통계적 가설 검정에서는 검정 통계량(test statistic)이라는 하나의 통계량을 구한다. 검정 통계량은 검정하고자 하는 가설에 맞춰 정의되는데,
t-검정에서는 아래의 수식처럼 평균을 가공한 값을 사용한다.
t-검정의 통계량은 t분포를 따르기 때문에 주로 T나 t로 부른다.

여기서 Sp는 합동 표준 편차(pooled standard deviation)이라고 불리는데, 두 분산을 결합한 것이라고 생각하면 된다. n은 각 집단의 표본의 크기이며, 검정통계량은 표본에 의해 정의되는 것이기 때문에 모평균 ${\mu}$가 아닌 표본평균 X̄에 관해 정의되었으며 n이 커짐에 따라 근사적으로 정규분포를 따른다. 직관적으로 보았을 때 검정 통계량 T는 두 집단 사이의 평균의 차를 표준편차를 이용해 적당히 가공한 값이다.
만약 T가 0에서 크게 벗어난다면 두 집단 사이의 차가 우연으로 볼 수 없을만큼 크다면, 우리는 두 집단의 평균이 다르다고 본다. 그리고 우연으로 볼 수 없을 만큼 얼마나 커야 하는지의 기준을 t분포를 통해 잡는데 주로 p-value나 신뢰구간을 이용한다.
Error(오류)
통계적 가설 검정은 항상 오류의 확률을 안고 있다.
공정한 주사위를 10번 던져서 모두 1이 나올 확률은 매우 낮긴 하지만 0은 아니다.
하지만 실제로 이를 경험한 사람은 주사위가 공정하지 않다고 할 것인데, 이를 통계학에서는 오류(error)라 한다.
이런 오류에는 두 가지가 있는데, 먼저 귀무가설이 맞는데 기각하는 경우를 1종 오류(Type1 Error)라 하고, 귀무가설이 틀렸는데 기각하지 못하는 경우를 2종 오류(Type2 Error)라 한다. 예를 들어, 신약의 효과가 없는데 효과가 있다고 결론짓는 것이 1종 오류이고, 신약이 실제 효과가 있는데 효과가 없다고 하는 것이 2종 오류이다.
연구의 맥락에 따라 어느 오류가 중요한 지 달라질 수 있지만, 일반적으로 통계학에서는 보통 1종 오류의 가능성을 고정하고 2종 오류를 최소화 한다. 이때 고정한 1종 오류의 가능성을 alpha(유의수준), 그리고 1-alpha, 즉 1종 오류가 일어나지 않을 가능성을 신뢰수준(confidence level)이라고 한다. 일반적으로 alpha를 0.05로 잡지만, 이것은 경험적인 것이며 분야와 맥락에 따라 달라질 수 있다.
추가로 2종 오류의 가능성을 beta라고 하고, 1-beta를 power(검정력)이라 한다.
일반적으로 통계 모형들은 주어진 alpha에서 beta를 최소화 하려고 하는데, 다르게 말하면 주어진 신뢰 수준에서 검정력을 최대화 한다고 말할 수 있다.
신뢰 수준이 주어지면 검정통계량을 가지고 최종 결론을 내릴 수 있다.
일반적으로 통계학에서는 p-value나 신뢰 구간을 이용한다.
P-value
먼저 p값은 개념적으로 귀무 가설이 맞다고 가정했을 때 데이터가 얼마나 극단적인지를 나타내는 값이다. 통계학에서는 주어진 데이터 혹은 주어진 데이터보다 더 극단적인 값이 나올 확률이라는 개념을 고안해냈고, 이것이 바로 p-value이다.
이렇게 구한 p값이 앞서 정한 신뢰수준보다 낮으면 귀무가설을 기각하고, 신뢰 수준보다 높으면 귀무가설을 기각하지 못한다.
예를 들어 동전 던지기 예시에서 앞면이 나올 확률을 p=0.5라 하면, 앞면이 나올 확률p 에 대해 신뢰구간을 구할텐데, 그 값을 대략 (0.44, 0.65)로 가정한다면, 귀무가설에서 가정한 p=0.5가 신뢰구간 안에 포함되기 때문에 귀무가설을 기각하지 못한다.
흥미로운 점 중 하나는, p값과 신뢰구간이 항상 같은 결론을 도출한다는 것이다.
💥 하지만 신뢰구간이 p값보다는 조금 더 직관적이고 많은 정보를 담고 있다고 볼 수 있다.
Reference
[Introduction to Basic Statistics in Python](https://wikidocs.net/book/7982)
'Mathmatics > Statistics' 카테고리의 다른 글
| ANOVA(Remedy) (0) | 2024.07.23 |
|---|---|
| Statistical Assumption (1) | 2024.07.01 |
| Statistical hypothesis test (0) | 2024.06.20 |
| Statistical Estimate (1) | 2024.06.14 |
| Continuous Probability Distribution (1) | 2024.06.09 |
